Mapas de Karnaugh
Criada pelo matemático George Boole no século XIX, a álgebra booleana se tornou fundamental para a criação de circuitos lógicos que viriam a ser utilizados em computadores digitais. Assim como a álgebra convencional, há uma série de padrões e teoremas que ajudam a "enxugar" uma expressão booleana, chegando à expressão mínima capaz de representar uma lógica sem nenhuma perda. É absolutamente possível basear-se apenas nesses padrões e teoremas para simplificar equações lógicas, mas há uma ferramenta gráfica que torna esse processo muito mais simples e capaz de ser representado de forma algorítmica.
Essa ferramenta foi criada nos anos 50 por Edward Veich e aperfeiçoada por Maurice Karnaugh, que dá o nome da versão que utilizamos até hoje. Estamos falando do mapa de Karnaugh. Esse mapa é, no fundo, uma representação da tabela verdade como um diagrama que busca agrupar os casos onde a saída do circuito é 1 e, assim, identificar padrões.
Código de Grey e a variação de bits
Uma das ferramentas que fazem o mapa de Karnaugh funcionar é o código de Grey. Honestamente, a explicação do código de Grey na Wikipedia está tão boa, que não estou achando que posso fazer melhor do que só adicionar o trecho aqui:
O código de Gray é um sistema de código binário inventado por Frank Gray. O código é não ponderado onde de um número para outro apenas um bit varia. Este sistema de codificação surgiu quando os circuitos lógicos digitais se realizavam com válvulas termoiônicas e dispositivos eletromecânicos. Os contadores necessitavam de potências muito elevadas e geravam ruído quando vários bits modificavam-se simultaneamente. O uso do código Gray garantiu que qualquer mudança variaria apenas um bit.[1]
Atualmente o código Gray é utilizado em sistemas sequenciais mediante o uso dos Mapas de Karnaugh, já que o princípio do desenho de buscar transições mais simples e rápidas segue vigente, apesar de que os problemas de ruído e potência tenham sido reduzidos.
A imagem abaixo representa o código de grey comparado com o sistema binário convencional.
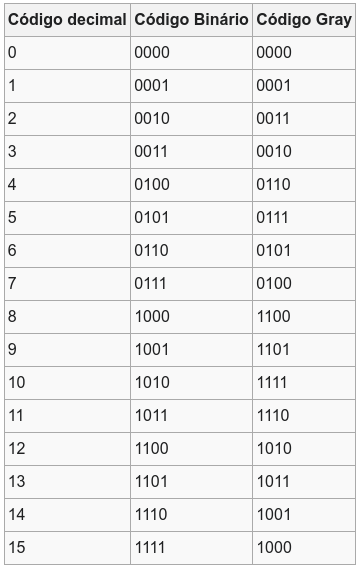
Mas o que o código de grey tem a ver com o mapa de Karnaugh? Ou melhor, por quê isso é útil? Vamos dar uma olhadinha em um mapa de Karnaugh e sua contrapartida em tabela verdade:
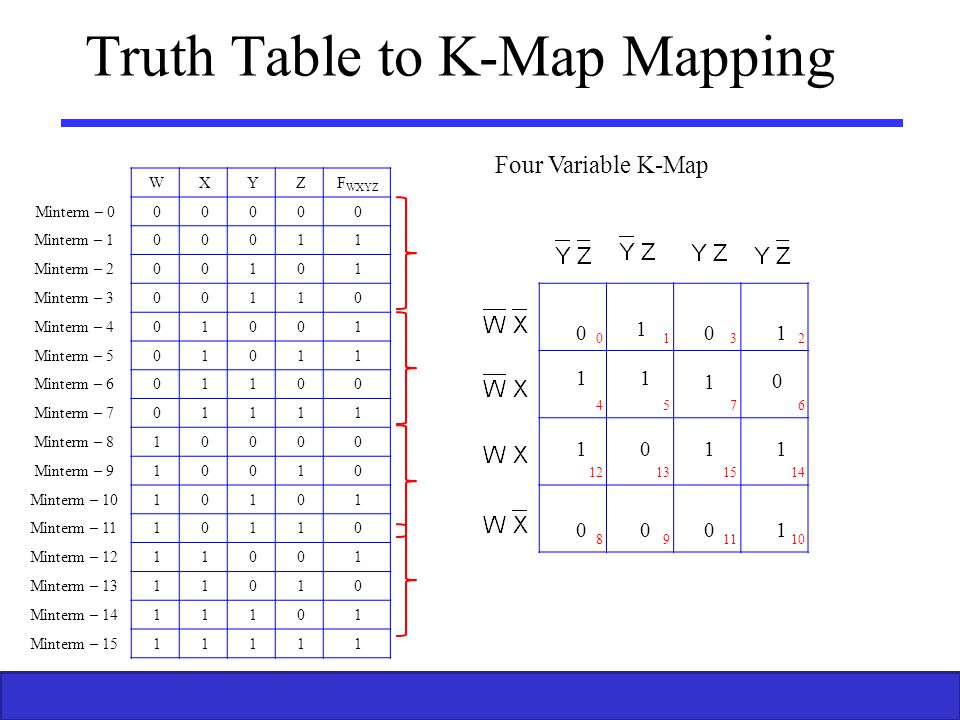
O motivo pelo qual o código de grey é interessante no mapa de Karnaugh é que a ideia é justamente que de uma coluna para outra e de uma linha para outra apenas uma variável mude. Assim, conseguimos identificar agrupamentos de 1 e verificar quais variáveis não variam nesse agrupamento. O que fazer quando notamos que a variável não varia no agrupamento? Simples, significa que ela não importa para aquele resultado e eliminamos ela.
A conversão do mapa de karnaugh para uma equação booleana pode ser feita a partir de um algoritmo. Deixei a tarefa de detalhar esse algoritmo para o GPT, mas também vou deixar um vídeo para vocês acompanharem o processo.
2.1. Algoritmo para Utilizar Mapas de Karnaugh (by GPT)
-
Construção do Mapa:
- Identifique o número de variáveis da função booleana a ser simplificada. Para n variáveis, o mapa terá 2^n células.
- Rotule as colunas e linhas do mapa com combinações de variáveis de forma que os estados adjacentes diferem por apenas um bit (Código de Gray).
- Transcreva os valores da tabela verdade para o mapa, colocando 1s nas células correspondentes às combinações de entrada que resultam em uma saída 1, e 0s para combinações que resultam em saída 0.
-
Identificação de Grupos:
- Procure por grupos de 1s (ou 0s, dependendo da simplificação desejada) adjacentes. As células podem ser agrupadas em potências de dois (1, 2, 4, 8, etc.). O objetivo é formar o menor número possível de grupos cobrindo todos os 1s (ou 0s).
- Os grupos podem se estender em linha reta ou envolver o mapa de uma borda a outra, pois o mapa de Karnaugh é considerado cíclico.
-
Derivação das Expressões Simplificadas:
- Para cada grupo de 1s, escreva o termo correspondente da expressão
booleana simplificada. Para isso, observe as variáveis que permanecem
constantes dentro do grupo:
- Se uma variável é 1 para todas as células no grupo, ela aparece na expressão como ela mesma.
- Se uma variável é 0 para todas as células no grupo, ela aparece na expressão como o seu complemento.
- Se uma variável muda de 0 para 1 (ou vice-versa) dentro do grupo, ela é ignorada no termo simplificado.
- Para cada grupo de 1s, escreva o termo correspondente da expressão
booleana simplificada. Para isso, observe as variáveis que permanecem
constantes dentro do grupo:
-
Construção da Expressão Final:
- Combine todos os termos obtidos de cada grupo utilizando a operação OR (para forma disjuntiva normal) ou AND (para forma conjuntiva normal).
-
Verificação e Ajustes:
- Certifique-se de que todos os 1s (ou 0s) estão cobertos pelos grupos formados. Caso contrário, revise os grupos para incluir todas as ocorrências necessárias.
- Revise a expressão final para garantir que está na forma mais simplificada possível.
Beleza. Agora que você viu como se usa um mapa de Karnaugh, vamos treinar um pouquinho?
Baseando-se na tabela verdade abaixo, crie um mapa de karnaugh para ela e extraia a equação lógica simplificada.
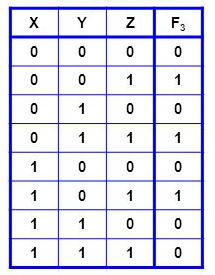
Baseando-se na tabela verdade abaixo, crie um mapa de karnaugh para ela e extraia a equação lógica simplificada.
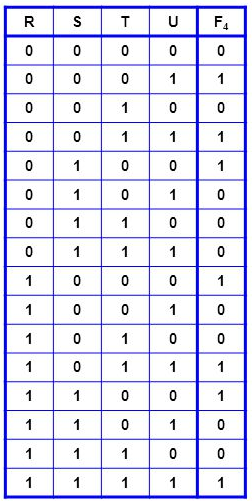
3. Circuitos lógicos
Quando falamos de circuitos lógicos, há dois tipos de circuitos distintos:
- Circuitos combinacionais
- Circuitos sequenciais
Ambos tem a sua importância para a computação. A seguir, vamos ver as definições dos dois tipos de circuitos e resolver alguns exercícios de ambos.
3.1. Circuitos combinacionais
Circuitos combinacionais são aqueles em que suas saídas dependem apenas da combinação de entradas atuais, sem qualquer tipo de temporalidade. Eles são utilizados em diversas aplicações, como aritmética, decodificação de sinais e roteamento de dados. Aqui estão alguns exemplos importantes:
- Encoder (Codificador): Um encoder é um circuito que converte informações de formato de entrada para um formato de saída codificado. Ele aceita várias entradas e gera uma saída binária que representa qual entrada está ativa. Um bom exemplo de circuito codificador é um multiplexador. O papel do multiplexador (ou mux, para os íntimos) é chavear sinais, utilizando uma entrada codificada para escolher qual dos sinais será "carregado" no circuito. Esse tipo de codificador é essencial para o funcionamento de microprocessadores. Abaixo, podemos ver um exemplo de multiplexador 4:1. Nele, temos as entradas X0 a X3, a saída M e os seletores C0 e C1.

Desenvolva o circuito lógico para o multiplexador acima.
Multiplexadores são absolutamente fundamentais para os microprocessadores. Por quê? Onde eles são utilizados dentro de um processador? Pesquise.
-
Decoder (Decodificador): Um decoder realiza a operação inversa de um encoder, convertendo uma entrada binária em um único sinal de saída ativado. Eles são amplamente utilizados em circuitos de memória para selecionar células de memória específicas, em displays de sete segmentos para mostrar números e em multiplexadores para determinar qual linha de dados deve ser conectada à saída.
-
Somador: Os somadores são circuitos combinacionais que realizam a adição de números binários. Existem dois tipos principais: o somador completo (full adder) e o meio-somador (half adder). Um meio-somador pode adicionar dois bits e produzir uma soma e um carry, enquanto um somador completo pode adicionar três bits (dois bits de entrada mais um carry-in). Somadores são componentes essenciais em processadores para realizar operações aritméticas.
Baseando-se na descrição acima e nas suas proprias pesquisas, desenvolva o circuito lógico de um meio-somador e um somador completo de 1 bit.
Extrapole o conhecimento adquirido sobre somadores e sua experiência resolvendo o exercício 5.06 para criar um somador de 4 bits.
Esses circuitos são utilizados em várias aplicações, como unidades aritméticas e lógicas (ALUs), sistemas de comunicação e em dispositivos de processamento de dados.