Introdução à circuitos lógicos

No século XIX, o matemático George Boole publicou o livro "An investigation of the Laws of Thought". O livro pontua seu interesse em formalizar um sistema algébrico - com símbolos e operações - para descrever a lógica. Até hoje, esse sistema é amplamente utilizado e recebe o nome de algebra booleana.

A álgebra booleana baseia-se em variáveis que podem assumir apenas dois valores; Verdadeiro ou Falso. Com essas variáveis, é possível realizar as seguintes operações:

1. Operação NOT - A operação de negação. Inverte o valor lógico de uma variável.
2. Operação AND - Operação de conjunção. Retorna verdadeiro apenas se todas as variáveis envolvidas forem verdadeiras.
3. Operação OR - Operação de disjunção. Retorna verdadeiro se pelo menos uma das variáveis envolvidas for verdadeira.
4. Operação XOR - Operação de exclusão. Retorna verdadeiro se apenas uma das variáveis envolvidas for verdadeira.

1. Princípios da algebra booleana

Assim como a álgebra à qual estamos acostumados, as operações típicas da álgebra booleana podem ser expressas utilizando símbolos. A saber:

• A operação AND empresta o símbolo da operação de multiplicação (. ou x);
• A operação OR empresta o símbolo da operação de soma (+);
• A operação NOT aparece como um traço sobre a variável (e.g. $\overline{A}$);
• A operação XOR utiliza o operador $\oplus$.

Também de forma análoga à álgebra convencional, há uma série de propriedades que permitem que uma expressão lógica seja simplificada.

Fig. - Propriedades da álgebra booleana.

Exercício

Uma propriedade interessante dos teoremas descritos acima (em particular o de DeMorgan) é que ele torna a função lógica NAND funcionalmente completa; isto significa que qualquer expressão lógica pode ser convertida em uma expressão que utiliza apenas a porta NAND. Vamos tentar provar isso?

Converta as portas lógicas a seguir de modo que elas sejam funcionalmente replicadas utilizando apenas portas NAND:

• NOT
• AND
• OR
• XOR

Como um exercício extra - pesquise por que essa propriedade é interessante na construção de chips de endereçamento de memória.

Na eletrônica digital, os circuitos que utilizam apenas combinações de operadores lógicos são denominados de circuitos combinatórios. Eles formam a base para as operações lógicas e aritméticas de uma CPU. Uma das ferramentas mais úteis para avaliar o comportamento de um circuito combinatório é a tabela verdade.

2. A tabela verdade

As tabelas verdade são uma ferramenta muito simples em sua essência: a sua razão de existir é mapear todas as combinações de entrada possíveis de um circuito lógico e obter a saída para cada uma delas. Para entender melhor como isso pode ser feito, vamos olhar uma das tabelas verdades mais simples possíveis, a do XOR:

Fig 5.01 - A porta lógica XOR e sua tabela verdade.

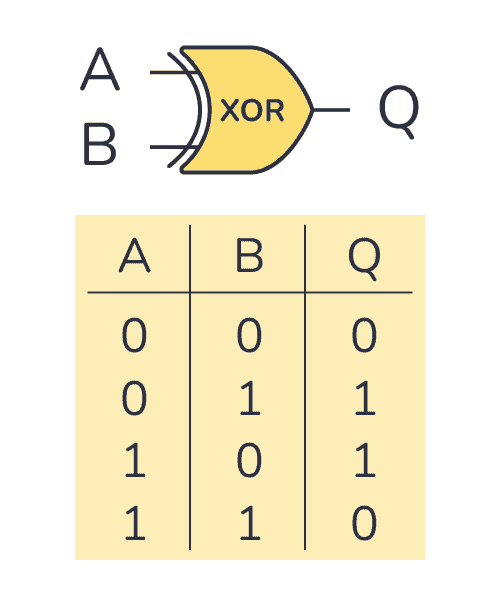
A primeira coisa que precisamos notar é a quantidade de linhas da tabela verdade. Isso tem uma relação direta com a quantidade de entradas do circuito. Essa relação se dá pela equação 2^n, onde n é a quantidade de entradas do sistema.

A seguir, preenchemos essas linhas com todas as comutações possíveis das entradas do circuito e, para cada uma dessas comutações, anotamos também se a saída é 1 ou 0. Vamos ver a tabela verdade de um exemplo um pouco mais complexo.

Fig 5.02 - Tabela verdade de um circuito lógico.

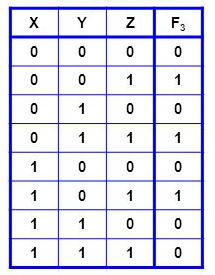
Logo de cara, é muito difícil dizer qual é esse circuito lógico. A maneira como você vai interagir com tabelas verdades é muito mais parecida com esse segundo exemplo do que com o primeiro, pois essa é uma ferramenta geralmente utilizada para a criação de circuitos lógicos que representam a lógica descrita pela tabela verdade.

Beleza, mas como fazer isso? É muito simples. Está vendo todas as linhas em que F3 é 1? Pegamos todas elas e "somamos" (leia-se, juntamos com portas OR). Dá uma olhada como isso fica:

$$F_3 = \bar{X} \cdot \bar{Y} \cdot Z + \bar{X} \cdot Y \cdot Z + X \cdot \bar{Y} \cdot \bar{Z}$$

info

Sim, eu notei que a equação está aparecendo duas vezes. É algum bug do katex que eu ainda não consegui resolver. Se algum de vocês souber o que é, por favor me avise.

Pronto, temos nossa equação lógica. Olha, eu sei que ela não parece muito otimizada e sei que você provavelmente já percebeu alguma forma de simplificá-la, mas vamos praticar o desapego até que a gente aprenda a usar o mapa de karnaugh? Beleza, boa. Mas antes disso, quero que você pratique com mais duas tabelas verdade.

Exercício

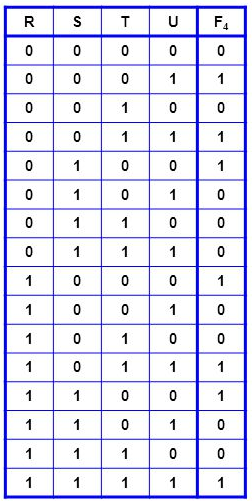
Baseando-se na tabela verdade abaixo, crie uma equação lógica que a represente.

Exercício

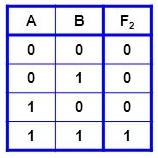
Baseando-se na tabela verdade abaixo, crie uma equação lógica que a represente.