O transistor como memória

Agora que já vimos como um transistor pode ser configurado para representar portas lógicas, precisamos entender como usar transistores como memória. O vídeo a seguir é bastante instrutivo e serve como um pontapé inicial para nossa discussão.

Autoestudo obrigatório

1. Lógica retroalimentada

Considere a seguinte situação, representada pela figura 9.01:

Fig 9.01 - Uma porta OR com uma das portas sendo retroalimentadas. O efeito é que o sistema é capaz de lembrar o valor 1.

Considerando o caso em que essa porta receba o sinal 0 na porta A e a segunda porta já esteja com valor 0, o que temos é uma situação de estabilidade. A saída é 0 e deve continuar assim. No entanto, se mudamos a porta A para 1, o que temos é uma instabilidade momentânea. O que se segue é um novo estado de estabilidade, com a saída em 1 e a segunda entrada como 1 também. Como a porta OR é dominada pelo sinal 1, não há mais como modificar o valor de saída dessa porta. Podemos dizer que esse circuito é capaz de armazenar o valor 1 em memória.

Exercício 9.01

Considere a mesma situação, só que utilizando uma porta AND. Em quais situações essa porta atinge estabilidade? Ela pode ser chamada de memória de 1 também?

2. Flip flops

2.1. Tipo RS

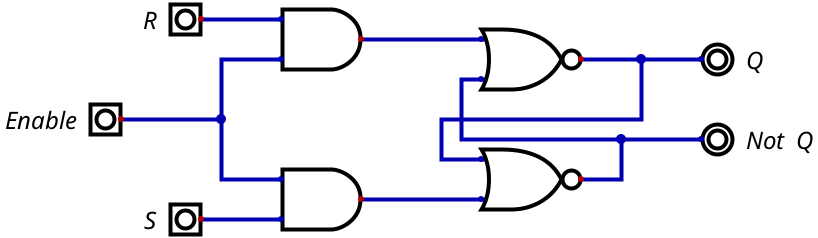
O circuito com a porta OR pode armazenar apenas valores 1, mas o que queremos com um circuito que atue como memória é ser capaz de armazenar tanto 0 como 1. Além disso, a porta OR retroalimentada nunca pode ser modificada depois que estabiliza com sua saída em 1. Apesar de existir diversos exemplos de memória de apenas escrita (ROM), esse tipo de memória tem um uso bastante limitado e não pode ser utilizado como registrador para a saída de uma operação aritmética da ALU, por exemplo. O que fazer? Bom, aí que entra o latch S-R. A figura abaixo representa o circuito em questão.

Fig 9.02 - O Latch Set-Reset funciona como uma memória de uso geral. Quando o sinal S é 1 e R é 0, o circuito estabiliza com Q = 1 e Not Q = 0. Quando R = 1 e S = 0, o circuito estabiliza com Q = 0 e Not Q = 1.

A figura 9.03 mostra a tabela verdade desse circuito. Como trata-se de um circuito em que a sequência de saída é importante, há duas colunas para a saída Q. Uma para o estado atual e uma para o estado futuro (N+1).

Fig 9.03 - A tabela verdade do latch SR.

Um dos problemas do circuito acima é que é imprevisível quando o circuito vai estabilizar sua saída. Uma solução para esse problema pode ser vista na figura 9.04 - o latch SR com sinal de enable.

Fig 9.04 - Adicionando um sinal de enable ao latch SR, é possível utilizá-lo como um sinal sincronizador.

Para entender como esse sinal de enable influencia no comportamento do latch SR, uma ferramenta útil para se utilizar é uma carta de tempos. A figura 9.05 exibe esse tipo de gráfico. Nele, o eixo y indica o nível lógico do sinal e o eixo x indica a passagem de tempo. O eixo x é comum para todos os sinais representados.

Fig 9.05 - A carta de tempo de um latch SR com enable. No gráfico, o sinal de enable está com o nome de Clock. Te faz lembrar de algo relacionado a computadores?

Exercício 9.02

Você é um aluno inteligente e já deve ter percebido que tem algo estranho nesse latch RS. Vamos falar sobre esse problema abertamente? O que acontece quando R e S são 1 simultâneamente? Nesse caso, a saída estabiliza em qual valor?

2.2. Tipo D

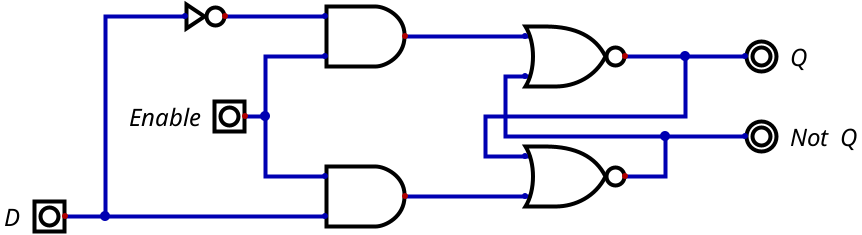
Agora que você já viu o problema do latch RS, vamos ver dois tipos de flip flops que resolvem esse problema? O primeiro deles é o flip flop tipo D. A ideia por trás dele é muito simples: se só tiver uma entrada, não tem como ter o conflito de entradas apresentado pelo latch SR. A figura 9.06 apresenta o circuito lógico de um flip flop tipo D.

Fig 9.06 - O flip flop tipo D(ata) é uma solução para o problema do latch SR. Com ele, é impossível atingir um estado em que o circuito fica instável. Incidentemente, a solução com apenas uma entrada faz com que esse circuito seja perfeito para construir registradores.

2.3. Tipo JK

Outra das soluções possíveis para o problema do R = 1 e S = 1 é apresentada pelo flip flop JK. Não, ele não foi inventado por Juscelino Kubitschek. A figura 9.07 mostra o circuito lógico do flip flop JK.

Fig 9.07 - O flip flop JK é a opção ideal para circuitos sequenciais. Seu uso é particularmente proeminente em contadores.

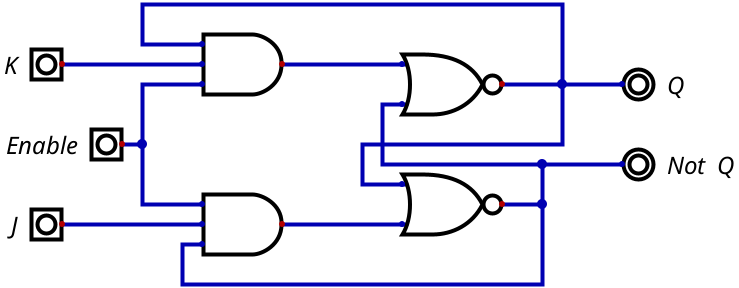
A figura 9.08 mostra a tabela verdade para o flip flop JK.

Fig 9.08 - Tabela verdade do flip flop JK. Nos casos em que os inputs J e K são iguais, em vez de estado indeterminado, temos inversão ou não do valor da saída.

Quando J = 1 e K = 0, Q estabiliza em Q = 1. Por outro lado, quando J = 0 e K = 1, Q estabiliza em Q = 0. Até aí, igualzinho ao latch SR. A diferença vem quando J = 0 e K = 0 ou J = 1 e K = 1. Na primeira situação, o valor de Q não se altera. Na segunda (que gerava uma situação indeterminada no latch SR), o valor de Q é invertido.

Exercício 9.03

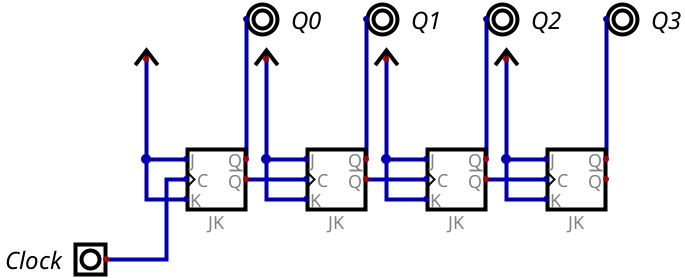
Desenhe uma carta de tempos para o circuito sequencial representado na imagem abaixo. Para isso, represente o sinal do clock como uma onda quadrada e represente as saídas Q0, Q1, Q2 e Q3. Qual conclusão você pode tirar a partir dessa analise?

Exercício 9.04

Utilizando flip flops JK e um único sinal de clock, crie um circuito contador decrescente de 4 bits (começa em 1111 e vai até 0000).

Exercício 9.05

Utilizando flip flops JK e um único sinal de clock, crie um circuito contador crescente de 4 bits que não tenha nenhum atraso. Em outra palavras, crie um contador síncrono.

Exercício 9.06

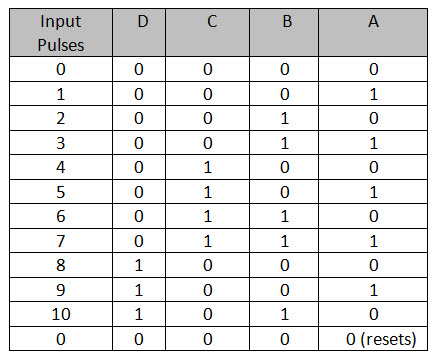
Crie um circuito sequencial que represente o comportamento de um contador de década. O contador de decada é um contador de 4 bits que vai de 0000 a 1010 e depois reseta.