Como representar números utilizando bits

Como vimos até então, o mundo digital opera exclusivamente em base 2 (binário). Isso significa que temos apenas os dígitos 0 e 1 disponíveis em vez dos 10 dígitos disponíveis no sistema decimal.

A conversão entre números de base 2 e base 10 é relativamente simples. A imagem abaixo exemplifica essa operação.

Fig 7.01 - Converter números binários para base decimal envolve a multiplicação de cada um dos dígitos por uma potência de 2. Começando em 0 e indo até n-1, em que n é a quantidade de dígitos do número.

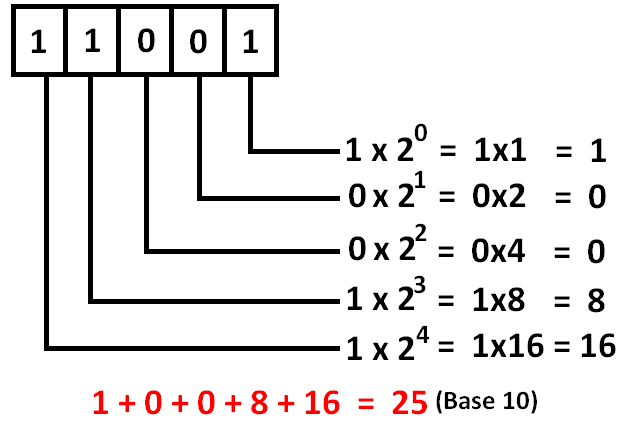
Vamos treinar um pouquinho?

Exercício 7.01

Converta o número a seguir de base 2 para base 10:

0010 1010

Exercício 7.02

Converta o número a seguir de base 2 para base 10:

1001 1110

Exercício 7.03

Nos exercícios anteriores eu tomei o cuidado de separar um número de 8 bits em duas partes iguais de 4 bits. Isso é uma prática comum principalmente no meio da computação. Por quê isso é conveniente? Qual a relação disso com a maneira como programamos computadores?

1. Números inteiros

A conversão acima já nos indica como é possível utilizar uma representação binária para valores inteiros, portanto não vou extender essa seção desnecessariamente. O que resta para nós? Bom, como podemos representar números negativos? Existem duas formas; utilizando sinal e magnitude ou utilizando complemento de dois.

1.1. Representação em sinal-magnitude

A representação por sinal-magnitude é talvez a mais intuitiva possível. Basicamente separamos o bit mais significativo do número inteiro para representar o sinal do número (se é negativo ou positivo). O restante do número é a magnitude dele. A figura abaixo demonstra essa forma de representação.

Fig 7.02 - Representação de números inteiros com sinal utilizando um bit de sinal e o resto para magnitude.

Exercício 7.04

Considerando números inteiros com sinal em representação de sinal-magnitude, converta o número abaixo para a base decimal:

1010 1100

Quando utilizamos essa forma de representação, a disposição dos números possíveis com 4 algarismos fica como disposto na figura abaixo.

Fig 7.03 - A disposição dos números inteiros possíveis utilizando a representação sinal-magnitude para 4 algarismos.

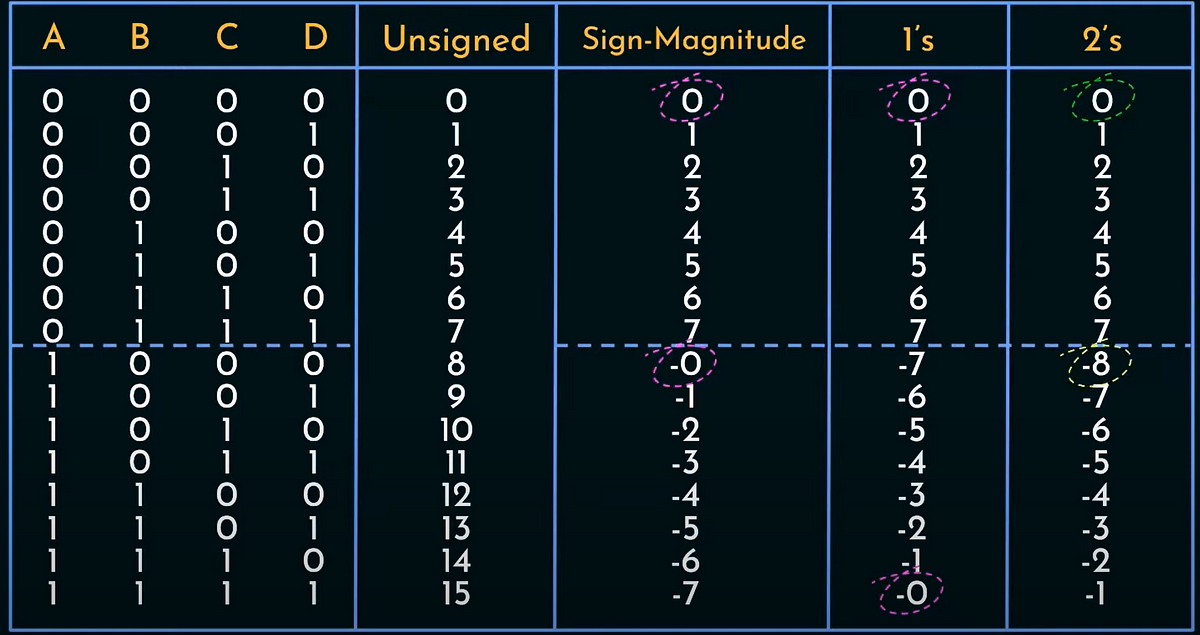
Apesar dessa representação ser bastante intuitiva, há dois principais problemas com ela:

1. Para operações de adição e subtração, precisamos primeiro verificar o bit de sinal sempre. Isso faz com que os circuitos combinacionais fiquem mais complexos.
2. Há duas formas distintas de representar o número 0. Uma das operações mais comuns na computação é justamente verificar se um número (ou resultado de operação) é 0. Ter duas representações distintas para este valor é bastante inconveniente.

Não por acaso, a representação sinal-magnitude não costuma ser utilizada na computação. Prefere-se utilizar a representação por complemento de dois.

1.2. Representação em complemento de dois

A representação por complemento de dois é muito parecida com a de sinal-magnitude. Começamos pelo bit mais significativo, que também indica o sinal do número. Onde está a diferença, então? Bom, vamos olhar novamente a Fig. 7.03. Notou que tem uma coluna lá chamada 2's? Pois bem, aquela é a coluna que mostra o valor em decimal para a representação em complemento de 2.

Perceba que o range de valores muda um pouco. Antes, tínhamos uma representação possível de -7 a 7. Com complemento de dois, podemos representar números de -8 a 7. O motivo disso é que eliminamos a possibilidade de representar -0. Além disso, é possível notar que a distribuição do complemento de dois está simétrica. Na representação sinal-magnitude, passamos direto do 7 para -0. Enquanto isso, na representação por complemento de dois, passamos de 7 para -8. Essa simetria é uma consequência de uma característica dessa representação que é muito útil para operações aritméticas. A figura 7.04 representa a distribuição de valores de uma forma em que essa simetria fica mais evidente.

Fig 7.04 - A distribuição de valores de um número de 4 algarismos em complemento de 2. Há uma simetria que permite com que os valores da distribuição sejam contínuos.

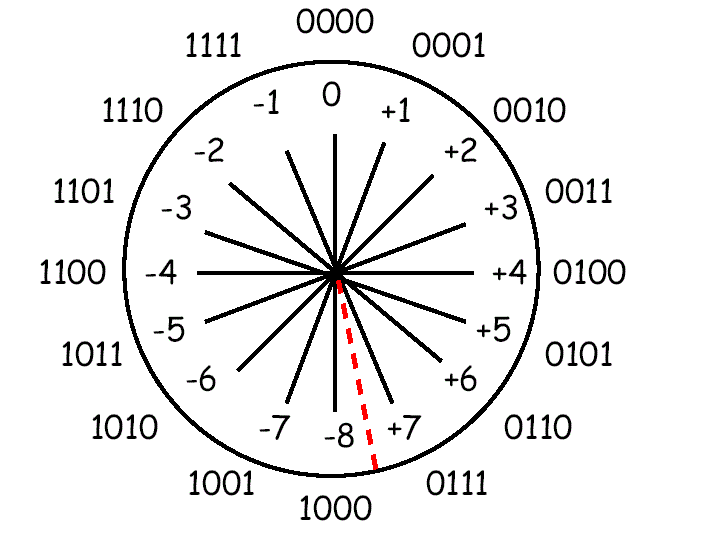
A característica ao qual me referia é uma particularidade na conversão entre números binários em complemento de dois para decimal. Vimos anteriormente que tipicamente a conversão binário-decimal envolve a soma de números dois com expoente referente à posição do algarismo (Figura 7.01). A figura 7.05 apresenta a versão atualizada da conversão, considerando a representação em complemento de dois.

Fig 7.05 - Diagrama de conversão de binário em complemento de 2 para base decimal. O bit mais significativo passa a valer como um número a ser subtraído do total.

Exercício 7.05

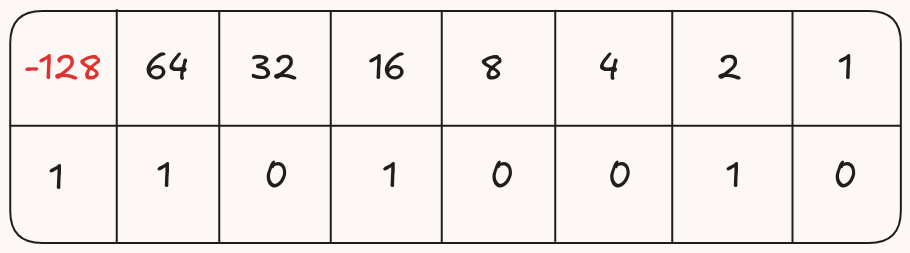
Converta o número binário acima em decimal. Considere que o número está representado utilizando complemento de dois.

A vantagem de usar a representação em complemento de dois fica mais evidente quando consideramos a operação artimética de subtração e adição. O que ocorre é que essa representação permite que a subtração seja o mesmo que a soma com um número negativo, simplificando os circuitos combinacionais necessários para implementar as operações artiméticas.

Exercício 7.06

Para que seja possível utilizar o complemento de dois na subtração, é importante ser capaz de inverter um número. Isso significa transformar um número positivo em sua contrapartida negativa e vice versa. O valor de 7 em binário, por exemplo, é 0111 e sua contrapartida negativa (-7) é 1001 em complemento de dois.

Existe uma sequência de operações relativamente simples para fazer essa conversão para qualquer número. Pesquise-a e teste-a com os seguintes números (use 8 bits):

• 24
• 123
• 0

2. Números reais

Boa parte dos valores que encontramos em problemas de cálculo numérico pertencem ao conjunto dos números reais e não dos inteiros. Sendo assim, é interessante discutir como podemos representar esses números em base 2. Para isso, vamos primeiro considerar com cuidado a maneira como representamos números fracionários em base 10. A figura 7.06 apresenta a maneira como trabalhamos com esse tipo de números.

Fig 7.06 - Números reais representados em base 10. Utilizamos uma representação em que separamos a parte inteira e a parte fracionária utilizando um delimitador.

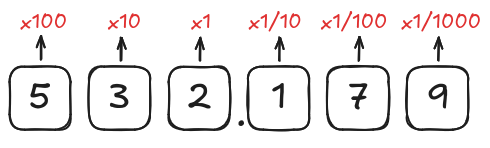
A maneira como lidamos com esses números é basicamente tratando a parte fracionária como uma soma de todas as frações em base 10. Podemos fazer a mesma coisa em base 2. O resultado pode ser visto na figura 7.07.

Fig 7.07 - Assim como trabalhamos com os números decimais, podemos utilizar números reais em base 2. Não é algo particularmente intuitivo pois não estamos acostumados a lidar com frações de base 2.

Exercício 7.07

Converta o número real representado acima para a base decimal

O problema? Não é exatamente uma forma eficiente de armazenar esses valores. Considerando o exemplo acima, em que temos 6 bits para representar os valores reais, a situação é a seguinte:

• Valor máximo possível - 7.875
• Valor mínimo possível - 0.125

Beleza, mas não vamos usar só 6 bits para representar esse número, né? Vamos considerar que um float típicamente é representado com 32 bits (4 bytes). Se utilizarmos 16 bits para guardar a parte inteira e 16 para a parte fracionária, temos:

• Valor máximo possível - 1023.9998919189
• Valor mínimo possível - 0.00001226452

Parece...bom, né? Calma aí. Note que não conseguimos chegar a números muito altos (~1024 é o máximo) e simultaneamente não chegamos nem em números tão pequenos assim. E isso sem nem considerar números negativos. Para colocar em perspectiva, se o valor mínimo possível fosse em metros, isso significaria que teríamos chegado apenas ao centésimo de milimetros. Isso não é o limite do aceitável para trabalhar com usinagem mecânica de precisão, quanto mais qualquer outra operação que necessite de uma precisão realmente alta.

2.1. Números de ponto flutuante

Vamos dar uma olhadinha nos valores reais do float?

• Valor máximo possível - 3.402823466 x 10^38
• Valor mínimo possível - 1.175494351 x 10^-38

Pera, o quê? Esse range é muito maior do que o que conseguimos na nossa representação!

Pois é. A maneira como o float é representado não tem nada a ver com aquela divisão de parte inteira e parte fracionária que vimos ali em cima. Na verdade, vou até roubar a definição da wikipedia em inglês para representação de pontos flutuantes. Acho que vai dar uma dica do que está acontecendo:

Na computação, aritmética de ponto flutuante é a aritmética que representa um subconjunto de números pertencentes ao conjunto dos números reais utilizando um valor inteiro de precisão fixa, chamado de significando, escalado por um inteiro expoente com uma base fixa. Números com esse formato são chamados de números de ponto flutuante. Por exemplo, o número 12.345 em formato de ponto flutuante com cinco dígitos de precisão e base 10 fica:

Fig 7.08 - Figura encontrada no artigo da wikipedia sobre aritmética de ponto flutuante.

Pois é. Números de ponto flutuante usam uma notação muito parecida com a notação científica e isso faz toda a diferença. Não, não é mágica. E sim, eu estou ciente de que não tem como representar uma quantidade maior de números com o mesmo número de bits. A genialidade dessa abordagem está na distribuição desses números. Veja a imagem 7.09:

Fig 7.09 - Distribuição de números possíveis de serem representados com a notação de pontos flutuantes. Há uma concentração de números possíveis perto de 0 e, conforme a magnitude do valor inteiro aumenta, os números possíveis se tornam mais esparsos.

Pois é... A resposta é simples quando vemos assim: basta usar mais desses números disponíveis quando a granularidade é mais importante. Isto é, quando o valor numérico está perto de zero. Por outro lado, quando o valor se aproxima do limite superior ou do limite inferior da notação, há cada vez menos granularidade nesses valores. Faz sentido, pois importa muito mais 0.00001 quando o valor total é 0.00021 do que quando é 2000000000.00001. O único ponto de atenção é que a mudança de float para double não é mais tão simples de decidir. Temos que olhar para a precisão e não mais para o range de valores possíveis.

Para encerrar essa incursão nos números reais representados em computador, vamos falar sobre um padrão. Afinal, eu posso escolher uma base diferente. De forma similar, posso escolher também tamanhos diferentes (em bits) para a base, expoente e significando. Entra o IEE 754.

2.3. Padrão IEEE 754

O vídeo abaixo mostra como funciona o padrão IEEE 754 para a representação de números de ponto flutuante na computação.

Autoestudo obrigatório

Vamos finalizar com alguns exercícios?

Exercício 7.08

Expresse os seguintes números em formato IEE de ponto flutuante com 32 bits:

1. -5
2. -6
3. -1,5
4. 384
5. 1/16
6. -1/32

Exercício 7.09

Considere um formato hipotético IEE de 7 bits, com 3 bits para o expoente e 3 bits para a mantissa. Quantos valores é possível representar? Qual o valor máximo? Qual o valor mínimo? Quais os dois valores mais próximos de 0 possíveis?